Visualizing and Summarizing Quantitative Variables

The story so far

Getting, prepping, and summarizing data

df = pd.read_csv("https://datasci112.stanford.edu/data/titanic.csv")
df["pclass"] = df["pclass"].astype("category")
df["survived"] = df["survived"].astype("category")

Marginal Distributions

If I choose a passenger at random, what is the probability they rode in 1st class?

marginal_class = df['pclass'].value_counts(normalize = True)
marginal_class
pclass
3    0.541635
1    0.246753
2    0.211612
Name: proportion, dtype: float64

Joint Distributions

If I choose a passenger at random, what is the probability they are a woman who rode in first class?

joint_class_sex = df[["pclass", "sex"]].value_counts(normalize=True).unstack()
joint_class_sex
sex       female      male
pclass                    
1       0.110008  0.136746
2       0.080978  0.130634
3       0.165011  0.376623

Conditional Distributions

If I choose a woman at random, what is the probability they rode in first class?

marginal_sex = df['sex'].value_counts(normalize = True)
joint_class_sex.divide(marginal_sex)
sex       female      male
pclass                    
1       0.309013  0.212337
2       0.227468  0.202847
3       0.463519  0.584816

Visualizing with the Grammar of Graphics

(ggplot(df, aes(x = "sex", fill = "pclass"))
+ geom_bar(position = "fill")
+ theme_classic()
)
<Figure Size: (1280 x 960)>

Quantitative Variables

We have analyzed a quantitative variable already. Where?

In the Colombia COVID data!

df_CO = pd.read_csv("http://dlsun.github.io/pods/data/covid/colombia_2020-05-28.csv")
df_CO
            Departamento  Edad  ... Fecha de diagnóstico Fecha recuperado
0            Bogotá D.C.    19  ...           2020-03-06       2020-03-13
1        Valle del Cauca    34  ...           2020-03-09       2020-03-19
2              Antioquia    50  ...           2020-03-09       2020-03-15
3              Antioquia    55  ...           2020-03-11       2020-03-26
4              Antioquia    25  ...           2020-03-11       2020-03-23
...                  ...   ...  ...                  ...              ...
25361  Buenaventura D.E.    48  ...           2020-05-28              NaN
25362    Valle del Cauca    55  ...           2020-05-28              NaN
25363  Buenaventura D.E.    39  ...           2020-05-28              NaN
25364    Valle del Cauca    13  ...           2020-05-28              NaN
25365            Córdoba     0  ...           2020-05-28              NaN

[25366 rows x 10 columns]

Visualizing One Quantitative Variable

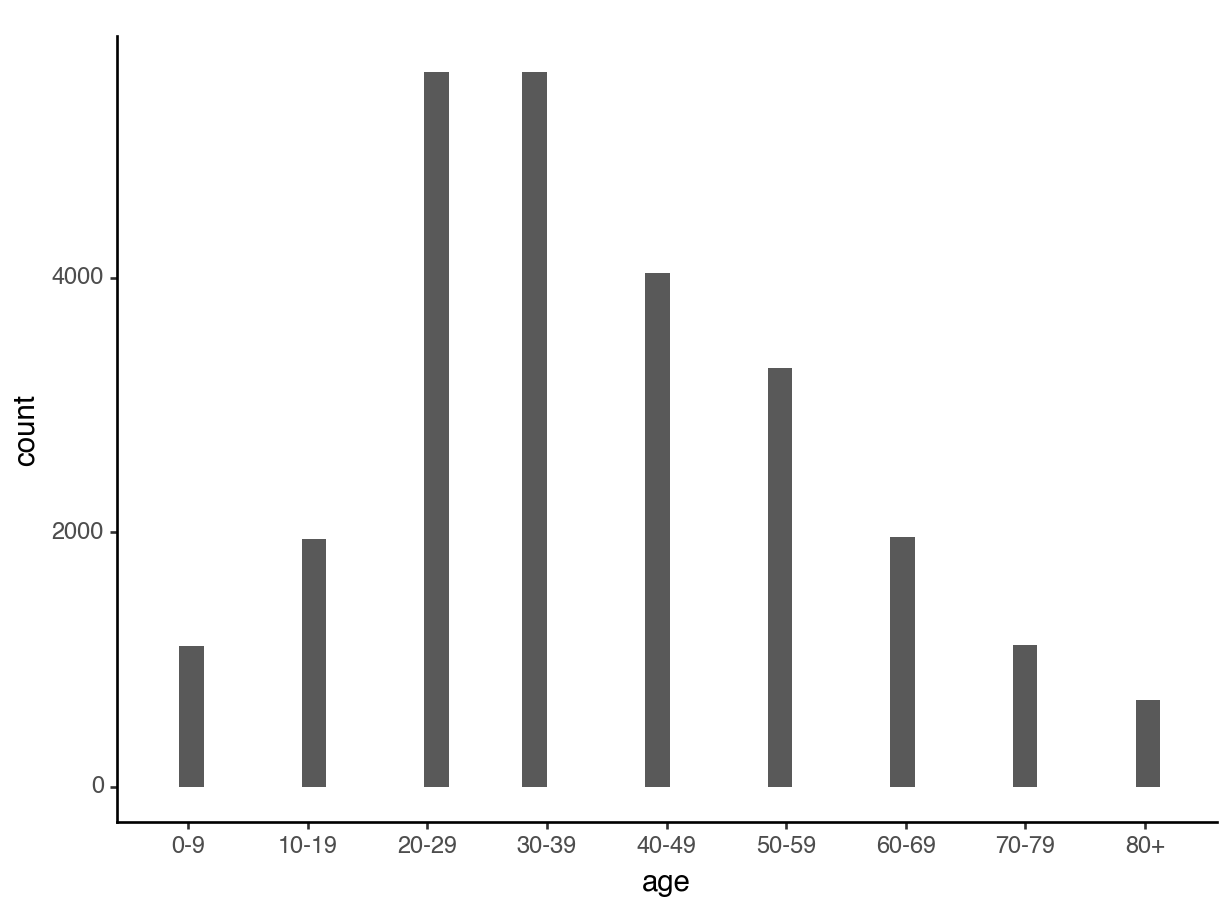
Option: Convert it to categorical

To visualize the age variable, we did the following:

df_CO["age"] = pd.cut(
    df_CO["Edad"],
    bins=[0, 10, 20, 30, 40, 50, 60, 70, 80, 120],
    labels=["0-9", "10-19", "20-29", "30-39", "40-49", "50-59", "60-69", "70-79", "80+"],
    right=False)

Option: Convert it to categorical

Then, we could treat age as categorical and make a barplot:

Code 
(ggplot(df_CO, aes(x = "age"))
+ geom_bar()
+ theme_classic()
)
<Figure Size: (1280 x 960)>

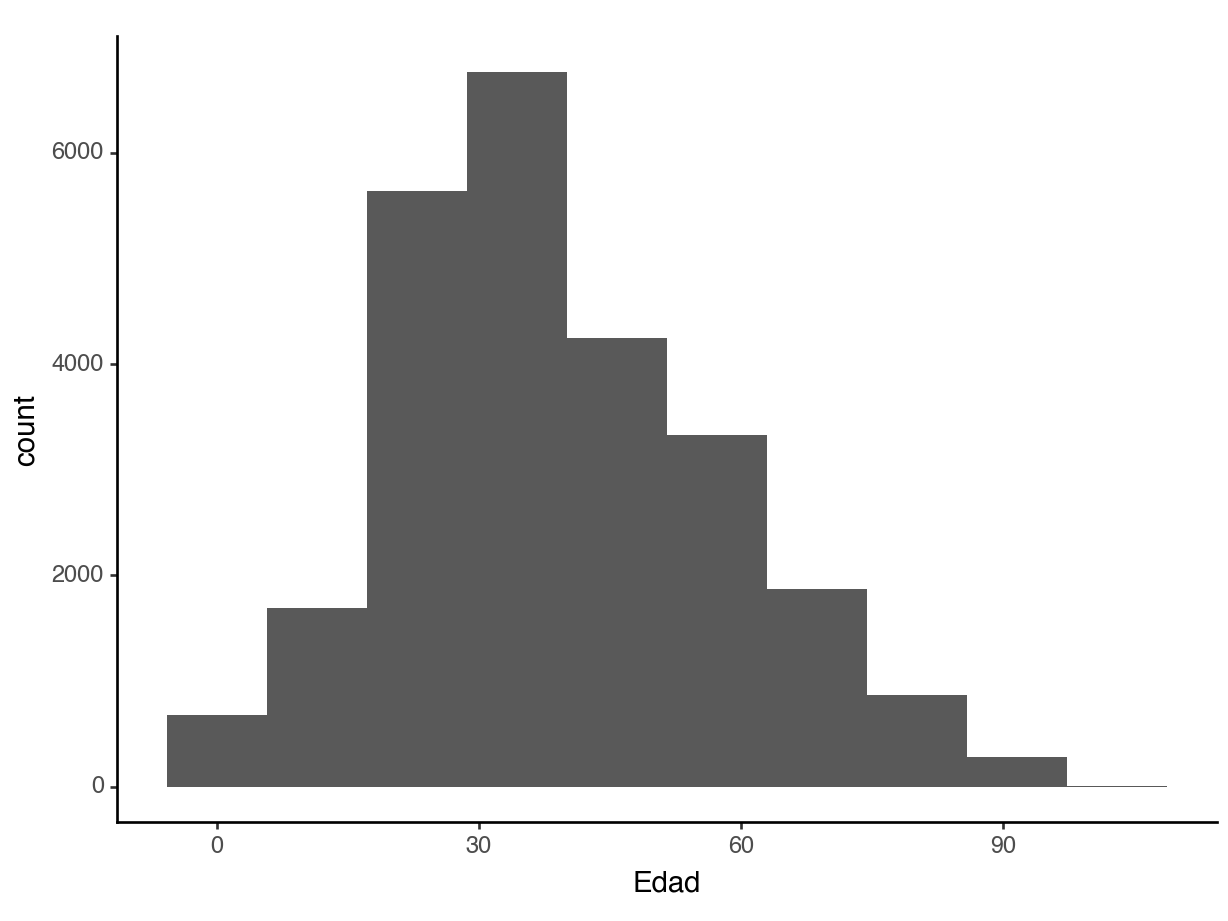
Better option: Histogram

A histogram uses equal sized bins to summarize a quantitative variable.

(ggplot(df_CO, aes(x = "Edad"))
+ geom_histogram()
+ theme_classic()
)
<Figure Size: (1280 x 960)>

Histogram

A histogram must use a quantitative variable to look right:

(ggplot(df_CO, aes(x = "age"))
+ geom_histogram()
+ theme_classic()
)
<Figure Size: (1280 x 960)>

Histogram

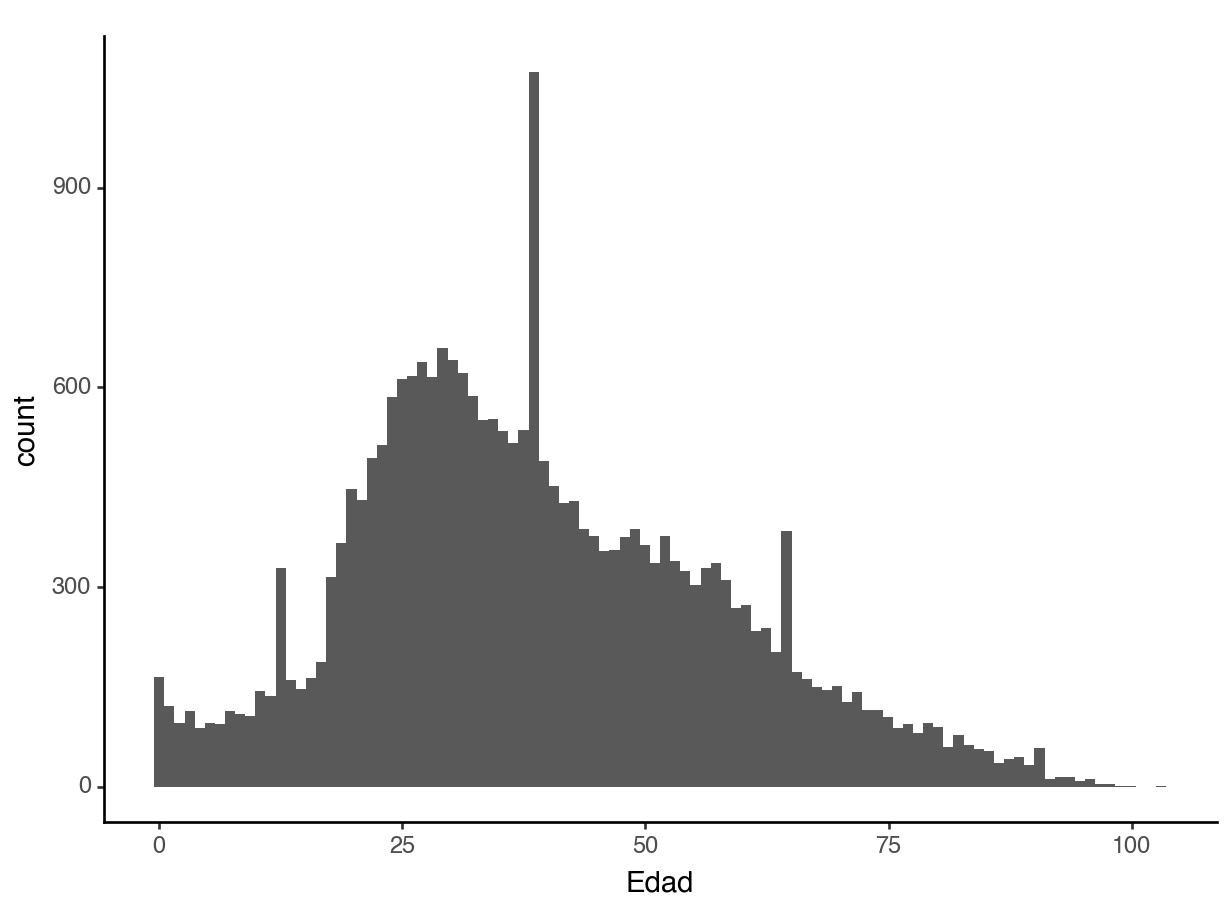
To tweak your histogram, you can change the number of bins:

Code 
(ggplot(df_CO, aes(x = "Edad"))
+ geom_histogram(bins = 10)
+ theme_classic()
)
<Figure Size: (1280 x 960)>

Code 
(ggplot(df_CO, aes(x = "Edad"))
+ geom_histogram(bins = 100)
+ theme_classic()
)
<Figure Size: (1280 x 960)>

Percents instead of counts

(ggplot(df_CO, aes(x = "Edad", y = '..density..'))
+ geom_histogram(bins = 10)
+ theme_classic()
)
<Figure Size: (1280 x 960)>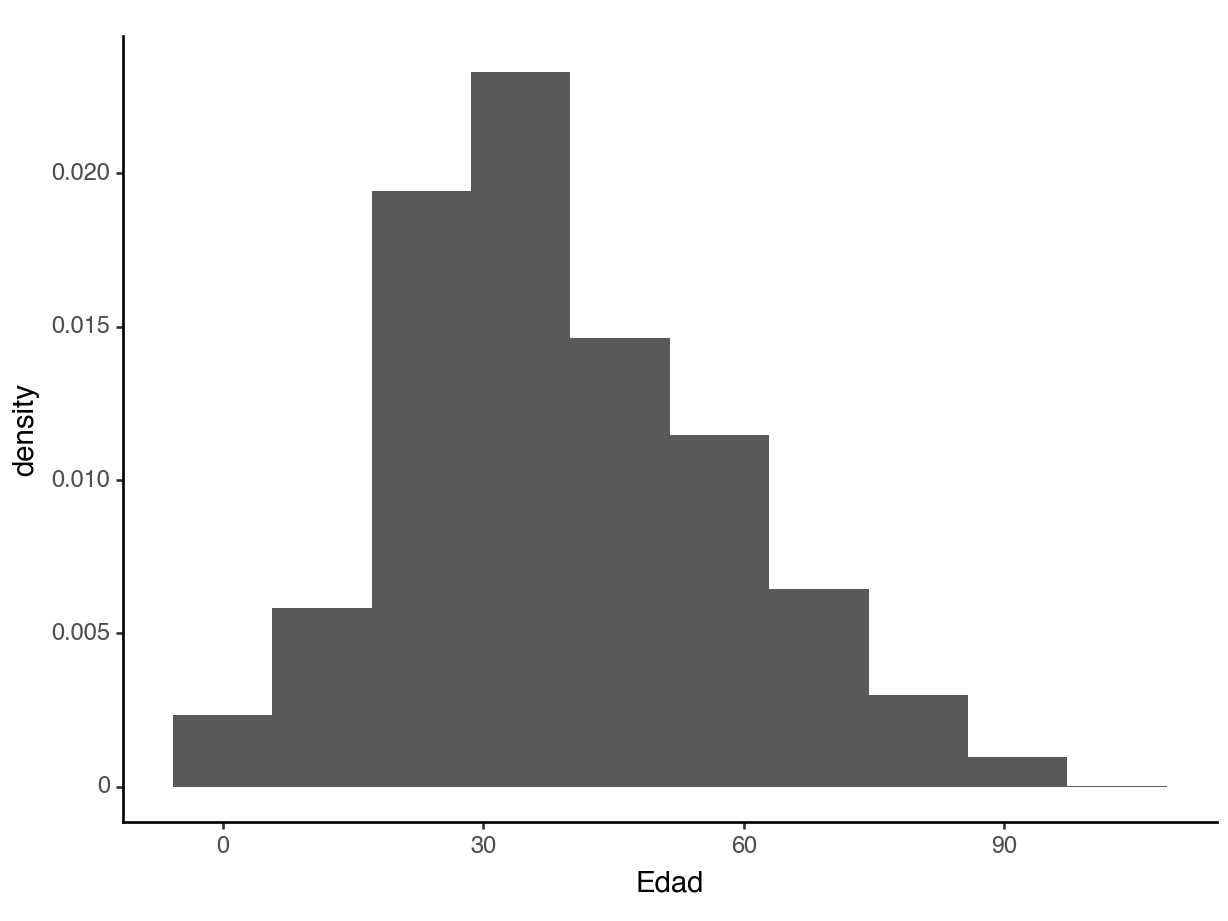

Distributions

  • Recall the distribution of a categorical variable: What are the possible values and how common is each?

  • The distribution of a quantitative variable is similar: The total area in the histogram is 1.0 (or 100%).

Code 
(ggplot(df_CO, aes(x = "Edad", y = '..density..'))
+ geom_histogram(bins = 10)
+ theme_classic()
)
<Figure Size: (1280 x 960)>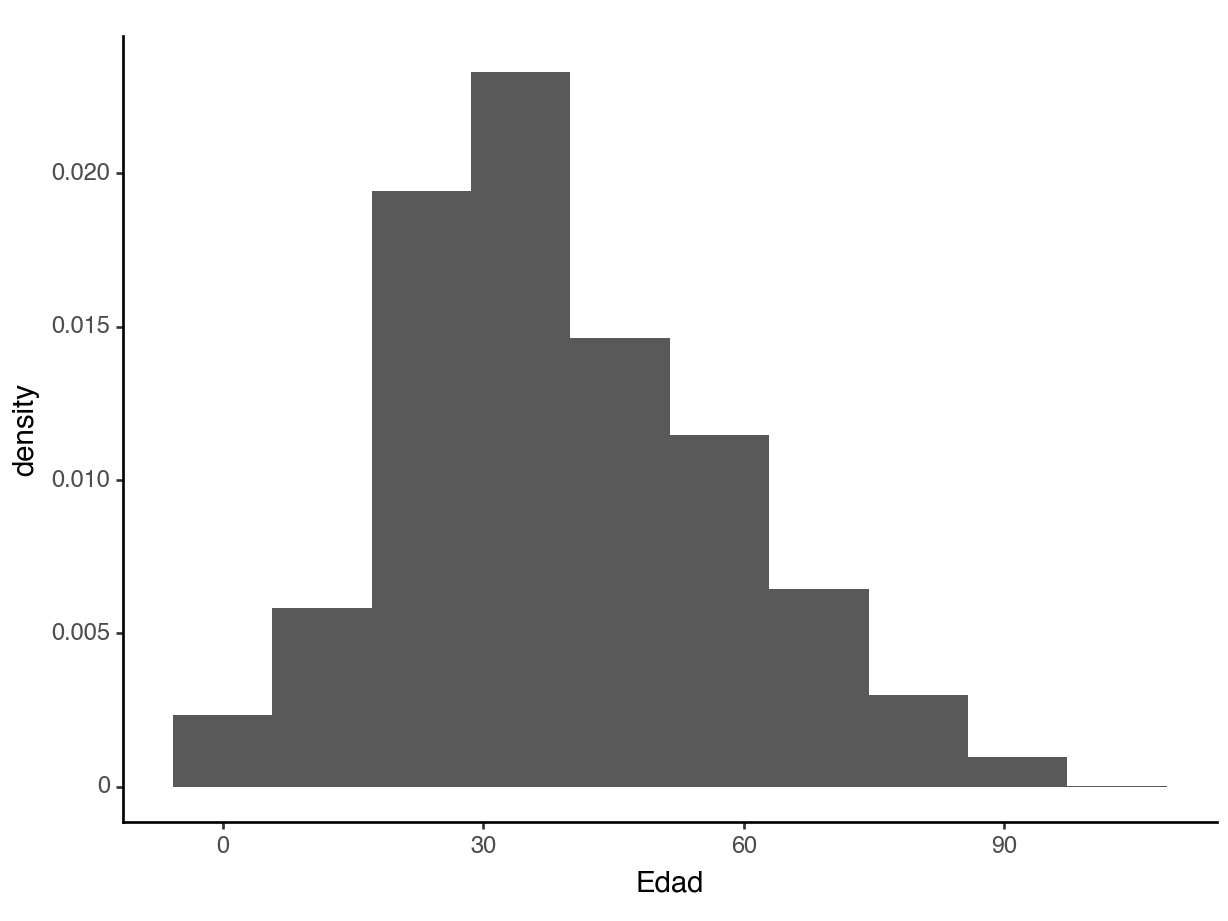

Densities

  • In this example, we have a limited set of possible values for age: 0, 1, 2, …., 100. We call this discrete.

  • What if had a quantitative variable with infinite values?

  • For example: Price of a ticket on Titanic.

  • We call this continuous.

  • In this case, it is not possible to list all possible values and how likely each one is.

    • One person paid $2.35
    • Two people paid $12.50
    • One person paid $34.98
    • …..?

  • Instead, we talk about ranges of values.

Densities

About what percent of people in this dataset are below 18?

Code 
(ggplot(df_CO, aes(x = "Edad", y = '..density..'))
+ geom_histogram(bins = 10)
+ theme_classic()
)
<Figure Size: (1280 x 960)>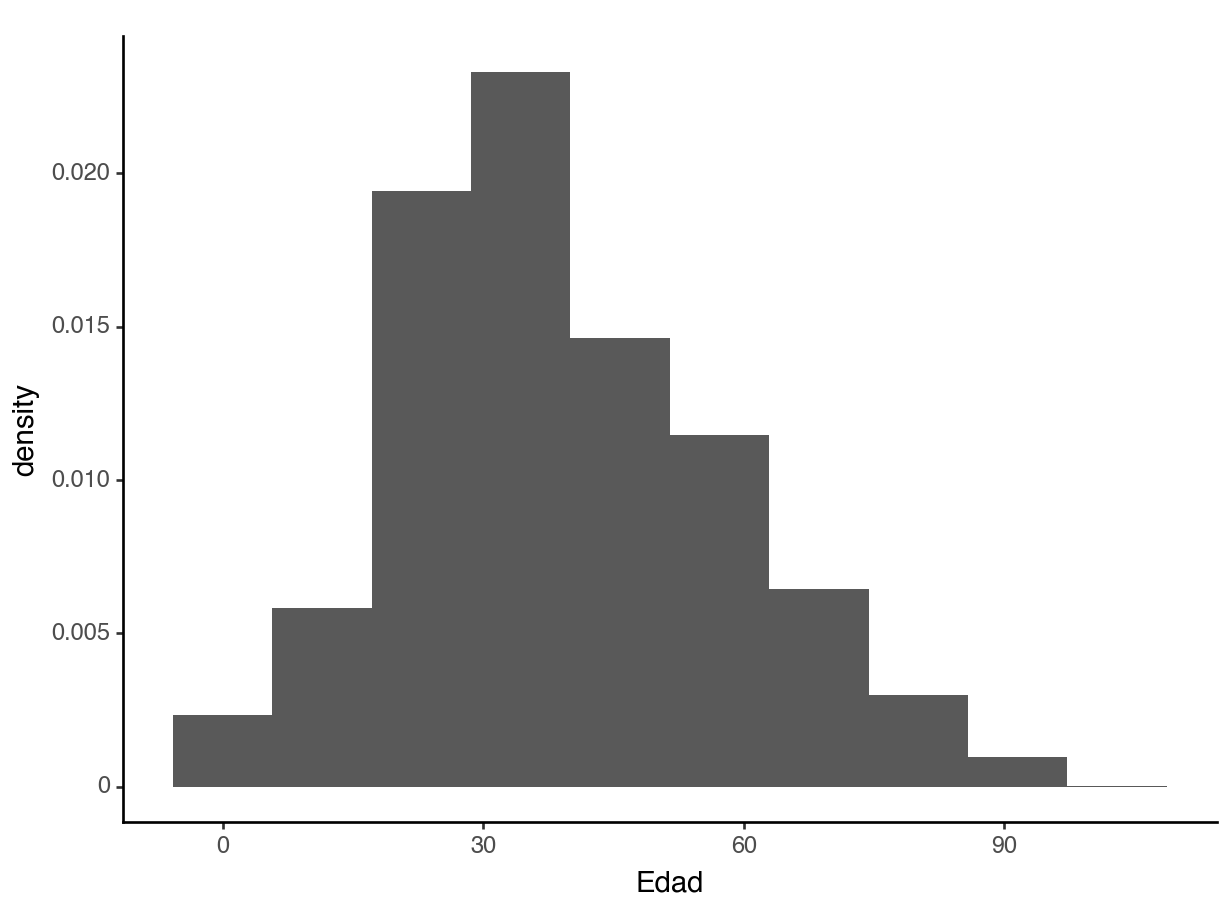

Densities

About what percent of people in this dataset are below 18?

Code 
(ggplot(df_CO, aes(x = "Edad"))
+ geom_density()
+ theme_classic()
)
<Figure Size: (1280 x 960)>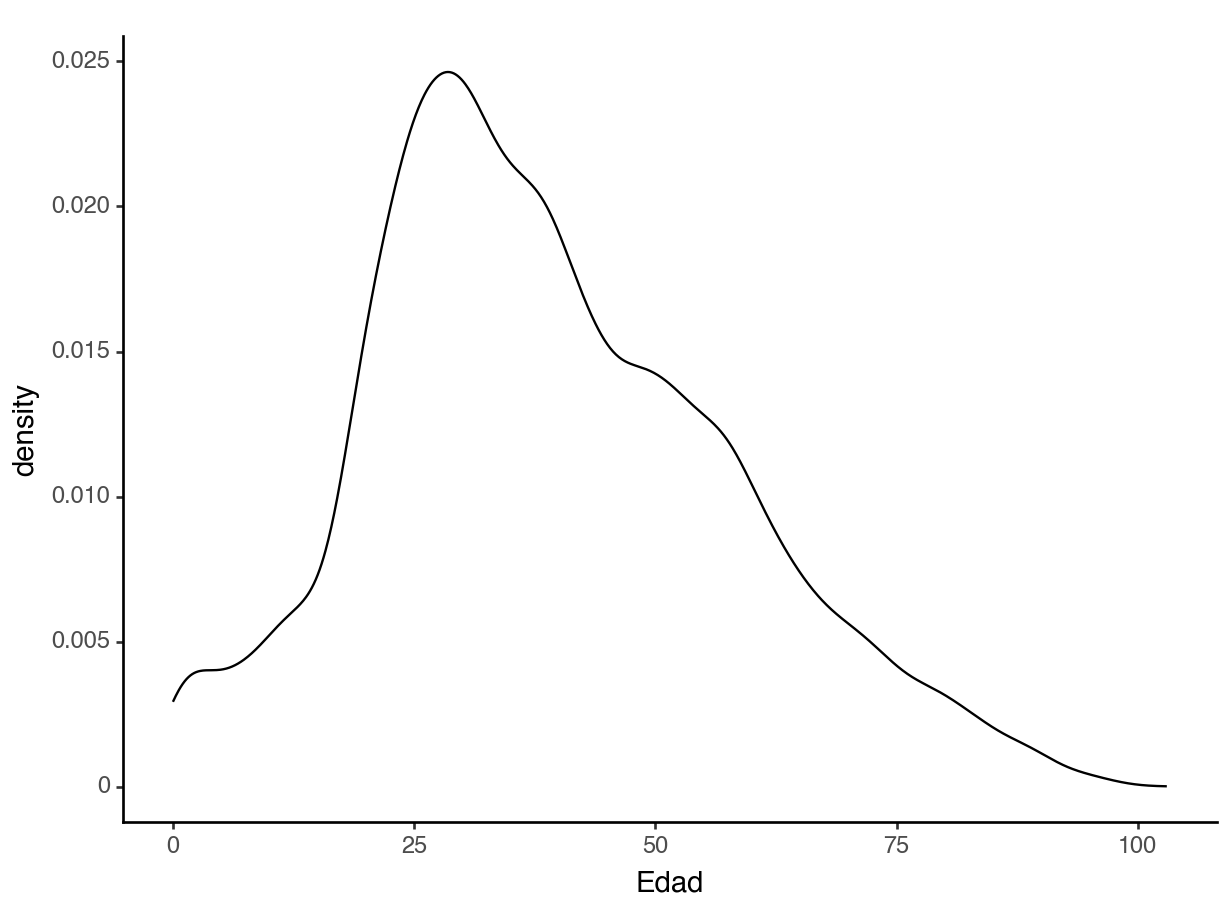

Summarizing One Quantitative Variable

Summarizing a Quantitative Variable

If you had to summarize this variable with one single number, how would you pick?

df_CO['Edad']
0        19
1        34
2        50
3        55
4        25
         ..
25361    48
25362    55
25363    39
25364    13
25365     0
Name: Edad, Length: 25366, dtype: int64

Summaries of Center: Mean

Mean

  • One summary of the center of a quantitative variable is the mean.

  • When you hear “The average age is…” or the “The average income is…”, this probably refers to the mean.

  • Suppose we have five people, ages: 4, 84, 12, 27, 7

  • The mean age is: \[(4 + 84 + 12 + 27 + 7)/5 = 134/5 = 26.8\]

Notation interlude

  • To refer to our data without having to list all the numbers, we use \(x_1, x_2, ..., x_n\)

  • In the previous example, \(x_1 = 4, x_2 = 84, x_3 = 12, x_4 = 27, x_5 = 7\). So, \(n = 5\).

  • To add up all the numbers, we use the summation notation: \[ \sum_{i = 1}^n x_i = 134\]

  • Therefore, the mean is: \[\bar{x} = \frac{1}{n} \sum_{i = 1}^n x_i\]

Means in python

Long version: find the sum and the number of observations

sum_age = df_CO["Edad"].sum()
n = len(df_CO)

sum_age/n
39.04742568792872

Short version: use the built-in function!

df_CO["Edad"].mean()
39.04742568792872

Activity

The mean is only one option for summarizing the center of a quantitative variable. It isn’t perfec!

Let’s investigate this.

  • Plot the density of ticket prices on titanic

  • Calculate the mean price

  • See how many people paid more than mean price

What happened

  • Our fare data was skewed right: Most values were small, but a few values were very large.

  • These large values “pull” the mean up; just how the value 84 pulled the average age up in our previous example.

  • So, why do we like the mean?

Squared Error

  • Recall: Ages 4, 84, 12, 27, 7.

  • Imagine that we had to “guess” the age of the next person.

  • If we guess 26.8, then our “squared error” for these five people is:

ages = np.array([4, 84, 12, 27, 7])
sq_error = (ages - 26.8)**2
sq_error.round(decimals = 1)
array([ 519.8, 3271.8,  219. ,    0. ,  392. ])
  • If we guess 20, then our “squared error” for these five people is:
sq_error = (ages - 20)**2
sq_error.round(decimals = 1)
array([ 256, 4096,   64,   49,  169])

Minimizing squared error

Code 
cs = range(1, 60)
sum_squared_distances = []

for c in cs:
  sum_squared_distances.append(((df_CO["Edad"] - c) ** 2).sum())

res_df = pd.DataFrame({"center": cs, "sq_error":sum_squared_distances})

(ggplot(res_df, aes(x = 'center', y = 'sq_error'))
+ geom_line())
<Figure Size: (1280 x 960)>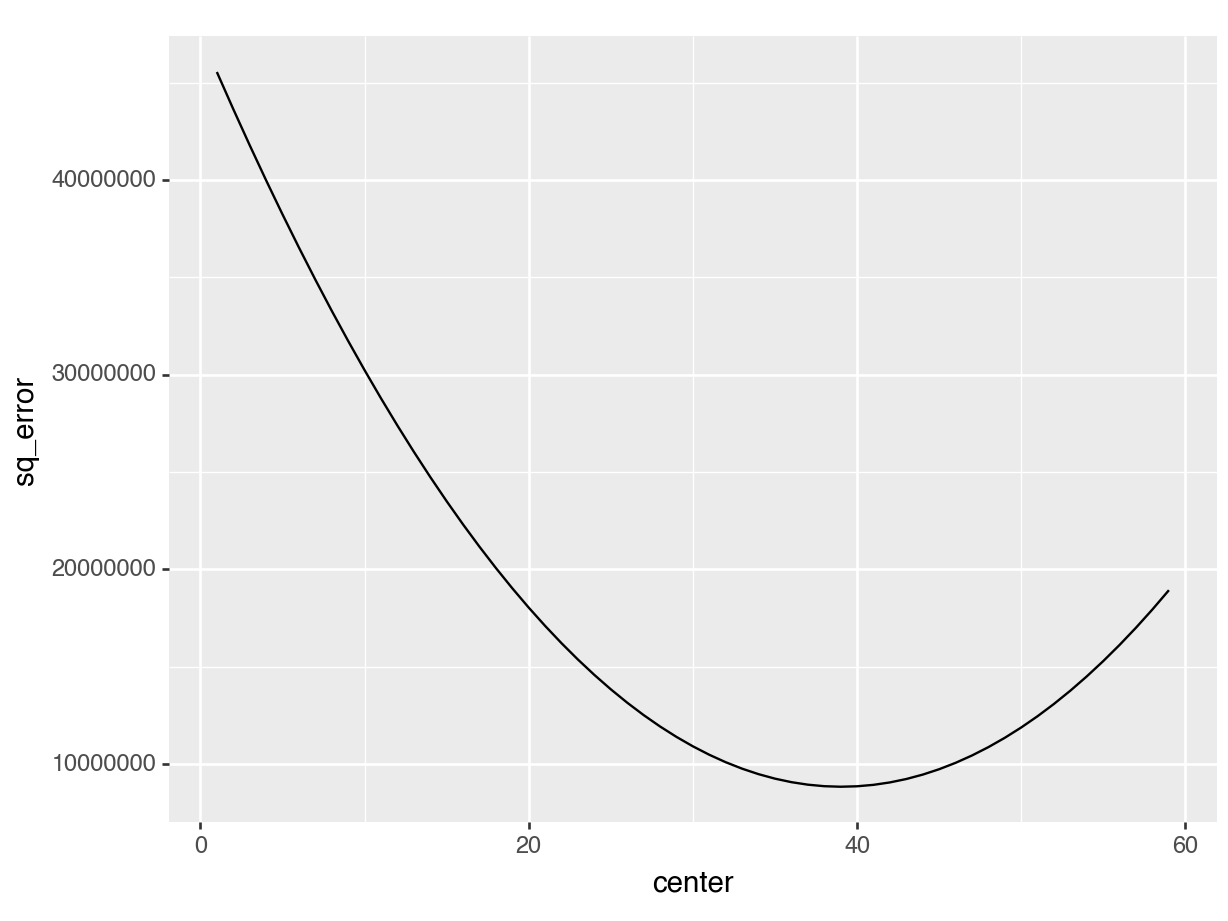

Summaries of Center: Median

Median

Another summary of center is the median, which is the “middle” of the sorted values.

To calculate the median of a quantitative variable with values \(x_1, x_2, x_3, ..., x_n\), we do the following steps:

  1. Sort the values from smallest to largest: \[x_{(1)}, x_{(2)}, x_{(3)}, ..., x_{(n)}.\]

  2. The “middle” value depends on whether we have an odd or an even number of observations.

    • If \(n\) is odd, then the middle value is \(x_{(\frac{n+1}{2})}\).

    • If \(n\) is even, then there are two middle values, \(x_{(\frac{n}{2})}\) and \(x_{(\frac{n}{2} + 1)}\). It is conventional to report the mean of the two values (but you can actually pick any value between them).

Median

Ages: 4, 84, 12, 7, 27. What is the median?

Median age in the Columbia data:

df_CO["Edad"].median()
37.0

Summaries of Spread: Variance

Variance

  • One measure of spread is the variance.

  • The variance of a variable whose values are \(x_1, x_2, x_3, ..., x_n\) is calculated using the formula \[\textrm{var(X)} = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1}\]

  • Does this look familiar? It’s the sum of squared error! (Divided by \(n-1\), the “degrees of freedom”)

Variance in python

We could do this manually:

(((df_CO["Edad"] - df_CO["Edad"].mean()) ** 2).sum() /
 (len(df_CO) - 1))
348.0870469898451

…or using a built-in Python function.

df_CO["Edad"].var()
348.0870469898451
348.0870469898451

Standard Deviation

  • Notice that the variance isn’t very intuitive: what do we mean by “The spread is 348”?

  • This is because it is the squared error!

  • So, to get it in more interpretable language, we take the square root:

np.sqrt(df_CO["Edad"].var())
18.65709106452142

Or, we use the built-in function!

df_CO["Edad"].std()
18.65709106452142

Takeaways

Takeaway Messages

  • Visualize quantitative variables with histograms or densities.

  • Summarize the center of a quantitative variable with mean or median.

  • Describe the shape of a quantitative variable with skew

  • Summarize the spread of a quantitative variable with the variance or the standard deviation.